We have two methods to estimate function: Maximum-likelihood (MLE) and Maximum-A-Posterior (MAP). We will consider MLE in this chapter, the latter will be told in Chapter 6. The discriminant function in Chapter 3:

It is easy to know because it is relative class frequencies, but
because it is relative class frequencies, but  is difficult. To estimate the likelihood, we can predict the kind of density function (Gaussian, Poisson, Uniform distribution, ...) and estimate that function as well as use the resulting estimates (for more exact result, we should consider mixed densities as we told in Chapter 2).
is difficult. To estimate the likelihood, we can predict the kind of density function (Gaussian, Poisson, Uniform distribution, ...) and estimate that function as well as use the resulting estimates (for more exact result, we should consider mixed densities as we told in Chapter 2).
 because it is relative class frequencies, but
because it is relative class frequencies, but  is difficult. To estimate the likelihood, we can predict the kind of density function (Gaussian, Poisson, Uniform distribution, ...) and estimate that function as well as use the resulting estimates (for more exact result, we should consider mixed densities as we told in Chapter 2).
is difficult. To estimate the likelihood, we can predict the kind of density function (Gaussian, Poisson, Uniform distribution, ...) and estimate that function as well as use the resulting estimates (for more exact result, we should consider mixed densities as we told in Chapter 2).
Because the unknown function  depends on a few parameters, so we transfer from the unknown-function estimating problem to the problem of estimating parameters of known-function. For example: Gaussian distribution we estimate mean(s) and (co-)variance.
depends on a few parameters, so we transfer from the unknown-function estimating problem to the problem of estimating parameters of known-function. For example: Gaussian distribution we estimate mean(s) and (co-)variance.
 depends on a few parameters, so we transfer from the unknown-function estimating problem to the problem of estimating parameters of known-function. For example: Gaussian distribution we estimate mean(s) and (co-)variance.
depends on a few parameters, so we transfer from the unknown-function estimating problem to the problem of estimating parameters of known-function. For example: Gaussian distribution we estimate mean(s) and (co-)variance.1. Maximum-Likelihood estimate (MLE)
MLE is maximizing the likelihood (the probability of obtaining the observed training samples). Informally interpreting, MLE chooses parameters to maximize  as discriminant function in Chapter 3. Let
as discriminant function in Chapter 3. Let  is parameter vector of class
is parameter vector of class  . For example, Gaussian density function (n-dimension):
. For example, Gaussian density function (n-dimension):
 as discriminant function in Chapter 3. Let
as discriminant function in Chapter 3. Let  is parameter vector of class
is parameter vector of class  . For example, Gaussian density function (n-dimension):
. For example, Gaussian density function (n-dimension):
Note that superscripts are not power of parameters, they illustrate i-th dimension. Because  depends on
depends on  , so
, so  =
= . Because we observe over several samples, so we let Di is training data, which contains samples of class
. Because we observe over several samples, so we let Di is training data, which contains samples of class  and transfer from maximizing
and transfer from maximizing problem to maximizing
problem to maximizing problem. Assume that Di give no information about
problem. Assume that Di give no information about if
if , so the parameters for the different classes are independent (in case of dependent parameters, we can use Hidden-Markov models). That is why we can work with each class separately, and eliminate the notation of class distinctions
, so the parameters for the different classes are independent (in case of dependent parameters, we can use Hidden-Markov models). That is why we can work with each class separately, and eliminate the notation of class distinctions  . Now, our task is transferred from maximizing
. Now, our task is transferred from maximizing problem to maximizing
problem to maximizing problem. Let D contains n samples: x1, x2, ..., xn. Since samples are independent, so:
problem. Let D contains n samples: x1, x2, ..., xn. Since samples are independent, so:
 depends on
depends on  , so
, so  =
= . Because we observe over several samples, so we let Di is training data, which contains samples of class
. Because we observe over several samples, so we let Di is training data, which contains samples of class  and transfer from maximizing
and transfer from maximizing problem to maximizing
problem to maximizing problem. Assume that Di give no information about
problem. Assume that Di give no information about if
if , so the parameters for the different classes are independent (in case of dependent parameters, we can use Hidden-Markov models). That is why we can work with each class separately, and eliminate the notation of class distinctions
, so the parameters for the different classes are independent (in case of dependent parameters, we can use Hidden-Markov models). That is why we can work with each class separately, and eliminate the notation of class distinctions  . Now, our task is transferred from maximizing
. Now, our task is transferred from maximizing problem to maximizing
problem to maximizing problem. Let D contains n samples: x1, x2, ..., xn. Since samples are independent, so:
problem. Let D contains n samples: x1, x2, ..., xn. Since samples are independent, so:
MLE will estimate by selecting optimal
by selecting optimal having the highest probability
having the highest probability . Intuitively, the value of
. Intuitively, the value of  best agrees with the actually observed training sample:
best agrees with the actually observed training sample:
 by selecting optimal
by selecting optimal having the highest probability
having the highest probability . Intuitively, the value of
. Intuitively, the value of  best agrees with the actually observed training sample:
best agrees with the actually observed training sample:
(*Source: Richard O.Duda et al. Pattern Recognition)
This means we find gradient of distribution density over parameters and set this gradient to be equal 0:
Inserting (1) to above equation:
To be convenient for analytical purposes, we will estimate with the logarithm of the likelihood than with the likelihood itself (especially Gaussian distribution).
Maximum likelihood corresponds to minimum negative log-likelihood due to functional form of log-function and probability values between 0 and 1.
with the logarithm of the likelihood than with the likelihood itself (especially Gaussian distribution).
Maximum likelihood corresponds to minimum negative log-likelihood due to functional form of log-function and probability values between 0 and 1.
 with the logarithm of the likelihood than with the likelihood itself (especially Gaussian distribution).
Maximum likelihood corresponds to minimum negative log-likelihood due to functional form of log-function and probability values between 0 and 1.
with the logarithm of the likelihood than with the likelihood itself (especially Gaussian distribution).
Maximum likelihood corresponds to minimum negative log-likelihood due to functional form of log-function and probability values between 0 and 1.
Because:
so (2):
Hence, the gradient of log-likelihood over parameters to be equal 0:
We will find optimal parameters from (3) in the next parts with different distribution density functions.
from (3) in the next parts with different distribution density functions.
 from (3) in the next parts with different distribution density functions.
from (3) in the next parts with different distribution density functions.2. MLE in Gaussian distribution (unknown mean)
We find optimal mean vector to maximize log-likelihood:
In general, we consider high-dimension Gaussian distribution:
Because the gradient of constant is 0, so we eliminate the first gradient:
If matrix A is symmetric, we have (for more detail):
Here, we apply chain-rule over :
:
 :
:
We insert (5) and (6) to (4):
To achieve the maximum-likelihood, the mean vector is the arithmetic average of the training samples.
3. MLE in Gaussian distribution (unknown mean and covariance)
We will find the gradient of log-likelihood over mean vector and covariance. Since the analysis of the multi-variate case is basically very similar to uni-variate case, we will consider uni-variate case and predict the results in multi-variate case.
We obtain the results:
and
From the above results, we have the results in multi-variate:
and
Both results are arithmetic average or expected value.
4. MLE in Poisson distribution
Likelihood of Poisson distribution:
Log-likelihood is:
The derivative of log-likelihood over lambda is equal 0:
The optimal parameter is the arithmetic average:
5. Summary
See Review on Chapter 5.











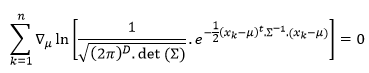






 is optimal mean vector. Since
is optimal mean vector. Since is not
is not 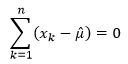













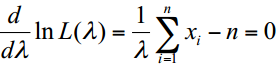











No comments:
Post a Comment