1. Discrete - Continuous random variable
1.1. Discrete random variable
Discrete random variable is a variable that can be any value in a set (sample space), which has a finite number of values.
X = {v1, v2, ..., vn}
The probability of random variable x is P(x), called probability mass function. P(x=vi) is the probability of value vi.
∑P(x=vi) = 1, with vi ∈ X
The expected value (mean) of a random variable x:
E[x]=μ =∑xP(x)
This means sum of weighting values based on the probabilities of the occurrence of these values or arithmetic average of x. In general, we replace x by f(x):
E[f(x)]=∑f(x)P(x)
From this general form, we can define variance. Variance measures how far values of x are likely to depart from the mean value.
1.2. Continuous random variable
Continuous random variable is a variable that can be any value in the continuum, which is a set having the infinite number of values. Because of infinite number of values, the probability of any particular exact value will almost always be zero. That is why we rather consider probability in the interval (a, b), called probability density function.
As we can see above figure, the probability of interval (4, 6) is a green region, which means we calculate the area of this green region. To calculate area limited by function curve and axes, we use integral.
Analogous to discrete random variable, mean is the sum of weighting values based on the probabilities of the occurrence of these values:
2. Statistical independence
2.1. Marginal distribution
Assume that we have two random variables:
V = {v1, v2, ..., vn} and U = {u1, u2, ..., um}
Joint probability of pair of (vi, uj) is the probability of the occurrence of vi event and uj event: Pr(x=vi,y=uj).
For example: Pr(x="playing_game",y="no_rain"), Pr(x="no_playing_game",y="rain")
The marginal distribution for x is given by summing over all y values or the probability of the occurrence of vi, not considering y values in detail:
2.2. Statistical independence
Statistical independence is that the knowledge of the value of x does not help us to infer the knowledge of the probability of y and vice versa or the probability of the occurrence of two events x and y is the product of the probability of each event that happens independently.
P(x,y)=Px(x,y) Py(x,y)
Example: Statistical independence
Px(x=0.6,y=0.4) Py(x=0.6,y=0.4)= 0.6 . 0.4 = 0.24 = P(x=0.6,y=0.4)
2.3. Covariance
The covariance of x and y is cross-variance that measures the level of statistical independence:
Covariance is normalized, called correlation coefficient:
If coefficient is +1 (or -1), then x and y are maximally positively (or negatively) related. x and y are un-correlated when coefficient is 0.
We see how covariance can measure the level of statistical independence:
(*Source: Rudolf Kruse et al. Texts in Computer Science)
In no correlation, knowledge of x does not improve our knowledge about y. In strong positive (negative) correlation case, the larger x is, the larger (smaller) y is. But covariance cannot measure exactly the level of statistical independence:
(*Source: https://en.wikipedia.org/wiki/Correlation_and_dependence)
In the last row, although x and y are dependent, but un-correlation. To address this problem, we can use mutual information to measure.
3. Conditional probability
3.1. Conditional probability
As we knew, statistical independence if and only if:
P(x,y)=P(x) P(y)
This means knowing x does not give us any additional information about the possibility of y. On the contract, in case of statistical dependence, we can receive more knowledge about the probability of y when we have known x or we can predict the value of y with a given value of x. That is why we need to change the above equation in case of dependence by replacing P(y) by P(y|x). P(y|x) is the probability of y if we know the value of x.
P(x,y)=P(x) P(y|x)
or
In case of independence, P(y|x) = P(y). In the other word, we do not need the knowledge of x to determine the probability of y.
3.2. Bayes rule
We have conditional probabilities:
and
so Bayes rule is:
The second equation is inserting P(x) / P(x) to P(x,y):
Terminology:
Evidence P(y) is marginal distribution, which is the probability of y over all values of x:
Because P(y) is the probability of y over all values of x, the evidence is independent on x => evidence is independent on the shape of distribution of P(x|y) and plays the role as normalization term.
As the equation of posterior calculation, we can compute posterior P(x|y) through likelihood P(y|x), which is invertible property of Bayes rule. We utilize invertible property of Bayes rule to determine P(x|y), which is difficult to estimate or unknown, via P(y|x), which is known and easy to estimate (because likelihood can compute from training samples).
For example, there is a man going to car store. How likely does he buy a Ferrari car, P(x=Ferrari|y=male)? It is difficult to estimate this probability because we cannot ask him how likely he buys Ferrari, he isn't a statistician. But we have already known how many percent of Ferrari car were bought by male customers in sale report, P(y=male|x=Ferrari).
3.3. Naive Bayes rule
In reality, we need to consider probability of a set of values P(x=v1,v2,...,vn|y=u1), not single value as the above example P(x=v1|y=u1). In the case of independent values, we use Naive Bayes rule. As we knew before, The joint probability of independent events equals to the product of the marginal probabilities of single event:
P(x1,x2,..., xn) = P(x1) P(x2) ... P(xn)
Analogous to the above case, the conditional probability of a set of values P(x=v1,v2,...,vn|y=u1) is:
P(x=v1,v2,...,vn|y=u1) = P(x1|y=u1) P(x2|y=u1) ... P(xn|y=u1)
The above equation is Naive Bayes rule. An example of usage of Naive Bayes rule is spam-mail filter. We assume that the probability of one word appearance is not influenced by other words in the mail or statistical independence.
P(word='hello', ...,'knock'|y=spam) = P('hello'|y=spam) ... P('knock'|y=spam)
However, words are meaningly dependent on other words, so we need to have other method. In practice, mutual information is used to determine how strong dependencies are and Hidden-Markov models is also used to determine the probabilities of a set of dependent values.
















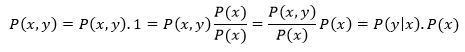











No comments:
Post a Comment