Explanation of self-attention (single head)

Attention (*Source: https://jasperwalshe.com/perspective-and-performance/)

1. Main ideas

Convolutional neural networks (CNN) only focus on local dependencies using kernel (the pink area as Figure 1), and dependent information (green pixel as Figure 1) beyond the range of kernel will be not considered. To take into account long dependencies, there are Recurrent neural networks (RNN). However, the stream of previous information are controlled by gates, so integrated information are include irrelevant information and relevant information are faded. Researcher suggested Bi-LSTM, or reversed the order of stream (Senquence-2-sequence) to mitigate this issue. Another suggestion is self-attention network (SAN) that takes into account global dependencies (except from limited-SAN that consider in the fixed range to reduce memory-consumption).

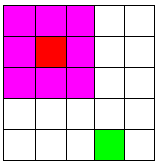
Figure 1. The dependent pixel is outside of the range of kernel in CNN.

The main idea of SAN is based on query-key-value. Think of dictionary in Python (or HashTable in Java). There are pairs of key-value as Figure 2. To retrieve information (value), user sends the query to machine. Machine lookup then all keys, choose the key which is exactly matched the query and retrieve corresponding value to respond user's request. As the Figure 2.a, the query of "water" is exactly matched the key of "water". Therefore, the information should be 100%*28.

Figure 2. Retrieve information by query-key. a. Query is exactly matched key. b. Query likely is matched key.

Likely, SAN will match query to key to determine which information are retrieved. However, it is, in practice, difficult to match exactly. Hence, SAN measures relationship between query and key that implies how likely the information that user needs. In the other words, this mechanism are considered as gate in RNN (but no matter of the locations of query and key). As Figure 2.b, the query of "H2O" is 80% matched the key of "water" and 20% matched the key of "rain". Hence, the information should be 80%*28 + 20%*46 = 31.6.

Figure 3. The model of Attention (single-head)

2. Architecture

As Figure 3, there are three main parts in the model of SAN: Linear transformation input (input becomes key, value and query via linear transformation), similarity calculation and weighted sum.

Firstly, why are there linear transformation? Their weights are trainable variables that learn the way to transform to new coordinates in which the dependencies are "visible" or easy to extract. Second reason is that linear transformation make sure new features (known as head) representing various aspects such that enriches diversity in the case of multi-head attention (each head represent a particular aspect). Note that, the weights in transformations of query, key and value are not shared variables. The below code show linear transformation.

# linear transformation
trans_k = tf.layers.dense(key_, args['n_hid_channel'])
trans_q = tf.layers.dense(query_, args['n_hid_channel'])
trans_v = tf.layers.dense(value_, args['n_in_channel'])

Of course, the value is the intensity of vector (gray level - Image Processing, word embedding - NLP or intensity of spectrum - Speech processing). Next, the similarity between key and query is the relationship between two locations in feature vector (a pixel - Image Processing, an embedding feature - NLP or a wave channel - Speech Processing). Here, SAN considers the intensity to be a metric to measure the level of relationship. Therefore, the input are became key, query and value after non-sharing linear transformation.

But, how to measure the above relationship? Self-attention uses dot-product to illustrate relationship or distance between key and query. The question is: Why dot-product?

Think about cosine distance. This distance measures the difference of angle as Figure 4, and the formula is in Equation 1.

Figure 4. Illustration of cosine distance. (*Source: https://www.machinelearningplus.com/nlp/cosine-similarity/)

Equation 1. Cosine distance.

The aim is that using cosine distance to measure similarity between key and query. We consider key and query as two vectors in the space. As Equation 1, cosine distance is dot product between two vectors (key and query), followed by normalization by their magnitudes. From that, cosine distance is equivalent to matrix multiplication, followed by sigmoid function. Hence, to convert to matrix operation, SAN firstly uses matrix multiplication which measure angle distance without normalization. SAN then normalizes this distance by using sigmoid function to generate value in the range of [0,1] (Sigmoid is consider as the gate that controls how much value is released).

# find dependencies using multiply of keys and queries
depend = tf.matmul(trans_q, trans_k, transpose_b=True)

# find similarity using softmax of dependencies

similarity = tf.nn.softmax(depend)

Finally, integrated information is weighted sum of value by using matrix multiplication between similarity coefficient and value.

# find head by multiply similarity by values

head = tf.matmul(similarity, trans_v)

To sum up, we will receive a new feature vector from input. However, this vector (head) only represents one aspect of global dependencies. To make it more diverse, we should use multi-head attention. I will cover this issue in the next blog.
Full code here: https://github.com/nhuthai/Feature-learning/tree/master/SAN

3. References

A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, I. Polosukhin, Attention is all you need. in NIPS 2017, 2017.