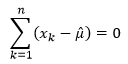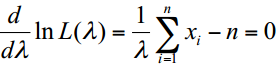Introduce Bayesian network

Yesterday, I took part in the Bayesian network seminar, presented by Stefan Conrady in Munich. I have learned the interesting knowledge: Bayesian network.

(*Source: Stefan Conrady - Bayesian Network Presentation)

As I mentioned in Chapter 1, Bayes rule illustrates the probability of dependent (and independent) probability, called conditional probability. In the real world, we have a lot of relationship factors, so the dependencies can be illustrated as networks, called Bayesian network.

For example, the result of exam influences on scholarship and my mood. The decision of going to bar based on scholarship (assume that I only gain money from scholarship) and my mood. If I go to bar, I would suit-up. Hence, from the above dependencies, I can build the network as the above picture.
The question is that why we need to use Bayesian network. Is it sexy? The answer is definitely "yes" (at least for my opinion).

1. Human and machine

In recent, many forums worry that the significant development of AI and Machine Learning leads the scenario that human under control by machines and robots. This could be because machine can learn easier and faster than human, especially human do not know what machine do or machine handle data as the blackbox. Bayesian network helps us to escape from this situation. There are interaction between human and machine during the process. Because human can understand through the network (see part 3), and it is understandable for machine to read network as the Directed Acyclic Graph.

(*Source: Stefan Conrady - Bayesian Network Presentation)

As the above figure, Machine Learning uses data to describe and predict the correlation. In contrast, human learns from theory to explain, simulate, optimize and attribute the causal relationship. The interaction between machine and human means machine describes and predicts from data (observation) and human then combine domain knowledge (part 2) to retrieve reasons (causal inference) through Bayesian network. Note that we cannot use data as reason (intervention), which will be explained in detail in part 5 through the example.

2. Compact the joint probability

One benefit we have when using Bayesian network is that reduce the unnecessary dependencies in joint probability. Back to the example of exam-clothes in introduction part, we have the joint probability:

p(exam,scholarship,mood,bar,suit-up) = p(suit-up|bar,scholarship,mood,exam) .  p(bar|scholarship,mood,exam) . p(scholarship|mood,exam) .  p(mood|exam)

Oops! It is so long and complicated! Imaging that what happens when we want to know the joint probability of 10,000 variables (example: the joint probability of dependent words).

To address this problem, we build Bayesian network by using domain knowledge, or our experience to reduce the dependencies (be careful with the difference between heuristic and biases). From my experience, the decision of suiting up does not involve to scholarship, my mood or the exam, and I will remove these dependencies. I continue to remove unnecessary dependencies:

p(exam,scholarship,mood,bar,suit-up) = p(suit-up|bar,scholarship,mood,exam) .  p(bar|scholarship,mood,exam) . p(scholarship|mood,exam) .  p(mood|exam)

Yeah! We cross out 5 dependencies from equation; therefore, the joint probability is compacted.

3. Formula visualization

I used to be very bad physics because of tons of formula that I need to remember. It was difficult to learn by heart all of them. I had an idea that I used graphs to illustrate the relationship between factors in formula. As a result, I understood and remembered these formula.Yesterday, I knew that I used to use Bayesian network to make formula easier to understand.

4. The curse of Dimensionality

In the 1D, 2D and 3D space, the nearer points have the lower distance. However, in the higher dimension, we can not use distance as the score to evaluate the nearest neighbors.
To explain it, we consider the distribution of A and B in D-dimension:

The distribution is the product of volume and average density of x in region A:

The volume is proportional to Radius and Dimension, let CD is the constant depends on number of dimension D:

Similar to region A, the density of region B:

Assume that the probability density in A is higher:

But x is more likely to belong to region B if dimension D=8:

This means x belongs to A, being far away from center of distribution. As a consequence, the distance measure, which becomes unreliable in higher dimensions.
Now, thanks to Bayesian network, we can compute its likelihood and avoid the distance measure.

5. Casual and Observational inference

I found that we are easily confused between observation and intervention. To be clearer, we will be back to the first example, I observe that my mood is influenced by the result of the exam. But now, there is no exam and I am rock-on, this means I do: p(mood=rock-on) = 100%

This confusion leads to a problem that I mentioned earlier in part 2 that we should not use the prediction from data as a reason. Here is an example to explain:

I will get the example in the presentation of Stefan Conrady on Bayesian network. People realized that the price of house will be proportional to the number of garages by linear regression:

(*Source: Stefan Conrady - Bayesian Network Presentation)

The wise owner thought that if he add two more garages, he would gain more $142,000.

(*Source: Stefan Conrady - Bayesian Network Presentation)

Oops!!! In fact the price of house does not increase since he did not observe, he did or intervene.

In the reality, we easily meet these faults as confounder, which makes mistakes in decision making especially medicine. For example: the doctor made a survey that coffee drinking causes lung cancer and concluded that coffee were not good for our lungs. But he did not that the coffee-aholic persons tend to smoke, which causes lung cancer.

Beside that, as Simpson's paradox, there are positive trends of variables in variety of groups, but the trend will be reversed when combining. This problem is caused by causal interpretation. For example: I assume data from some supermarket:

As above table, there is a conclusion that male customers tend to buy more than female. However, we consider the report for each store, it is very weird:

Looking at the above table, almost female customers tend to buy the goods in the stores which have fewer visitors. This is causal interpretation. 

To sum up, correlation does not causation. Simpson's paradox points out that the correlation of two variables are positive, but in fact they are negatively correlated by the "lurking" confounder. Here is not artificial intelligence, that is human intelligence. That is why we need to combine artificial intelligence and human intelligence, which can be done via Bayesian network.

Review Techfest Munich 2017

I took part in Hackathon Techfest Munich at TU Munich in September, 2017. This was the first time I joined Hackathon. It was really interesting.

1. Activities

This Hackathon was more than Hackathon with many disciplines, which is not only for software developers, but also for biologists, business, media, .etc. It is great idea because we can learn together and practice to work in the multi-discipline environment.

In the first day, a presentation was held to introduce to participants about themes of this competition. Then, they divided into smaller groups and organize seminar to explain in detail. Especially, they asked participants to write down their ideas and to present. It is a good idea since those who did not have any idea have a chance to brainstorm their idea or choose the ideas from others to establish and work in the following days.

We work during 3 days with awesome support from organizers such as hardware, food, drink, .etc.

Beside project-related activities, we enjoyed many funny and crazy events there.

2. Feeling and the future

I used to be introvert person, scare to communicate to strangers. But I changed a lot, I made a lot of friends there. It was really one of the most amazing events I have joined.

After this event, I learned that if I have an crazy ideas, I just share to our community. I should not bother the implement beyond my knowledge since the mentors and team-mates would help me. Before that, I had many ideas, but I had worried I could not implement because I am software developers, not biologist or hardware engineer.

After all, I have idea that why not we organize these kinds of Hackathon for children, which help them determine their potential career in the future. In my country, high-school students do not decide their career objective since they do not clearly know about which job they would like to study and work. They usually decide well-paid jobs or high-rated jobs. In Vietnam, doctor and banking officer are the most very-highly-rated jobs and many good students chose this job since they want to be respected regardless of their interest. As a result, they could not graduated or find their jobs. Hence, Hackathon is a good idea to help children choose their right job.

Finally, I write this blog with the hope that students can join these events like this event to expand their network and experience more challenges.

Review Pattern Recognition Chapter 5: Maximum-Likelihood estimation

Chapter 5 is very complicated to understand. That is why I publish this blog to summarize the knowledge in the Chapter 5.
Basically, we have a look on mindmap:

Second option is a video with an example I have made:


Hopefully, you have fun to learn this chapter.

Pattern Recognition - Chapter 5: Maximum-Likelihood estimation

We talked about Bayesian decision rule in Chapter 3, in which we assumed that x is a scalar or 1-dimension and we have known the exact density function. In reality, we have to make decision based on many criteria (so x is a feature vector or high dimension) and we do not know the perfect and exact density function. The former problem that we addressed in Chapter 4 and the latter will be considered in this chapter.
We have two methods to estimate function: Maximum-likelihood (MLE) and Maximum-A-Posterior (MAP). We will consider MLE in this chapter, the latter will be told in Chapter 6. The discriminant function in Chapter 3:

It is easy to know because it is relative class frequencies, but  is difficult. To estimate the likelihood, we can predict the kind of density function (Gaussian, Poisson, Uniform distribution, ...) and estimate that function as well as use the resulting estimates (for more exact result, we should consider mixed densities as we told in Chapter 2).

Because the unknown function  depends on a few parameters, so we transfer from the unknown-function estimating problem to the problem of estimating parameters of known-function. For example: Gaussian distribution we estimate mean(s) and (co-)variance.

1. Maximum-Likelihood estimate (MLE)

MLE is maximizing the likelihood (the probability of obtaining the observed training samples). Informally interpreting, MLE chooses parameters to maximize  as discriminant function in Chapter 3. Let is parameter vector of class . For example, Gaussian density function (n-dimension):

Note that superscripts are not power of parameters, they illustrate i-th dimension. Because  depends on , so =. Because we observe over several samples, so we let Di is training data, which contains samples of class  and transfer from maximizingproblem to maximizingproblem. Assume that Di give no information aboutif, so the parameters for the different classes are independent (in case of dependent parameters, we can use Hidden-Markov models). That is why we can work with each class separately, and eliminate the notation of class distinctions . Now, our task is transferred from maximizingproblem to maximizingproblem. Let D contains n samples: x1, x2, ..., xn. Since samples are independent, so:

(1)

MLE will estimateby selecting optimalhaving the highest probability. Intuitively, the value of  best agrees with the actually observed training sample:

(*Source: Richard O.Duda et al. Pattern Recognition)

This means we find gradient of distribution density over parameters and set this gradient to be equal 0:

Inserting (1) to above equation:

To be convenient for analytical purposes, we will estimatewith the logarithm of the likelihood than with the likelihood itself (especially Gaussian distribution). Maximum likelihood corresponds to minimum negative log-likelihood due to functional form of log-function and probability values between 0 and 1.

(2)

Because:

so (2):

Hence, the gradient of log-likelihood over parameters to be equal 0:

(3)

We will find optimal parametersfrom (3) in the next parts with different distribution density functions.

2. MLE in Gaussian distribution (unknown mean)

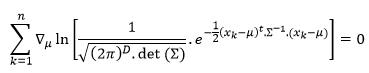
We find optimal mean vector to maximize log-likelihood:

In general, we consider high-dimension Gaussian distribution:

Because the gradient of constant is 0, so we eliminate the first gradient:

(4)

If matrix A is symmetric, we have (for more detail):

(5)

Here, we apply chain-rule over:

(6)

We insert (5) and (6) to (4):

Whereis optimal mean vector. Sinceis not zero-matrix, so:

To achieve the maximum-likelihood, the mean vector is the arithmetic average of the training samples.

3. MLE in Gaussian distribution (unknown mean and covariance)

We will find the gradient of log-likelihood over mean vector and covariance. Since the analysis of the multi-variate case is basically very similar to uni-variate case, we will consider uni-variate case and predict the results in multi-variate case.

We obtain the results:

and

From the above results, we have the results in multi-variate:

and

Both results are arithmetic average or expected value.

4. MLE in Poisson distribution

Likelihood of Poisson distribution:

Log-likelihood is:

The derivative of log-likelihood over lambda is equal 0:

The optimal parameter is the arithmetic average:

5. Summary

See Review on Chapter 5.